
A Brief Discussion of the Engineering Principles
Used in the Design of Camming Devices for Rock Climbing
By: Vaino V. Kodas
The following discussion assumes a little familiarity with rock-climbing equipment and basic engineering concepts.
The shape of the cams on a typical camming device is given by the formula: r = eµø
r is the radius
e is the natural logarithm base
µ is a coefficient which determines how "fast" the spiral opens up (and it has more interesting significance, as seen later)
ø is the angle measured in radians.
Plotting the formula above, using polar coordinates, results in the shape shown in Figure 1. This shape is known as a logarithmic spiral, or an equiangular spiral. This means that any straight line drawn from the center outward in any direction intersects the curve at one constant angle.
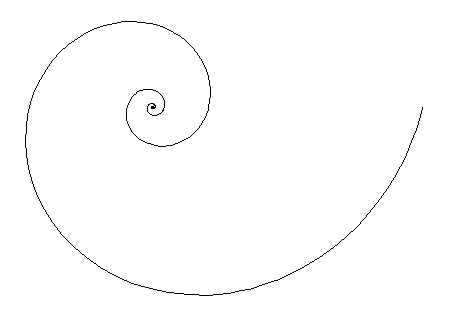
Figure 1
A typical camming device uses cams whose outer surface follows the contour of a sector of this curve. The pin, or axle, around which the cams rotate is the center, or (0,0) point of the graph. In Figure 2 below, a camming device is shown placed inside a parallel-walled crack. The handle (not shown) pulls down on the center pin and transfers the load to the walls of the crack (shown in blue) via the opposing cams.
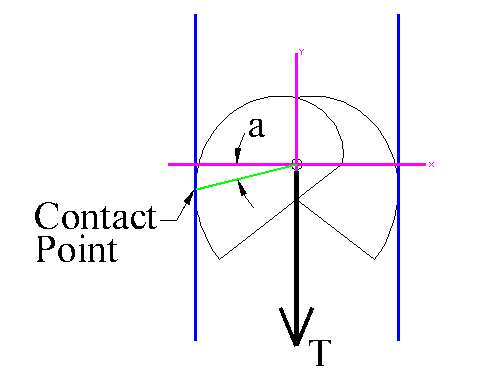
Figure 2
From an engineering standpoint, the most important information would be the contact angle (a), which can be seen to be the constant angle of the equiangular spiral. With a little mathematics (an interesting exercise, left to the reader) one can find that this angle (a) is given by a = tan-1(µ) regardless of how far the cams are retracted.
Figure 3 shows a free body diagram depicting the forces on the pin at the center of the cams.
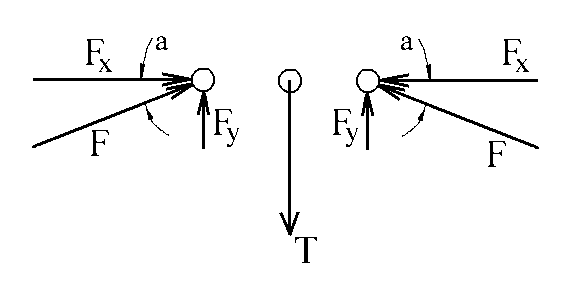
Figure 3
Summing forces in the vertical direction,
we get Fy = T/2. Also, we know tan(a) = Fy/Fx.
Combining these two equations gives Fx = T/2tan(a). Then,
since a = tan-1(µ), we get Fx = T/2µ
and
F = (T/2)*SQRT(1+1/µ2)
Careful measurement reveals that most camming devices used in rock climbing are made with a spiral where µ is about .25 (and therefore angle a is about 14 degrees).
This means that when µ = .25 (as on most camming devices used for rock climbing) Fx = 2T
Physically, this means that when a tension T is applied downward on the shaft of a camming unit placed in a parallel walled crack, the resulting outward force on each of the walls is about 2T (depending on the exact value of µ). In other words, the spreading force is twice the force that is pulling down.
The above equations were derived for only one set of opposing cams. If there were two cams in each direction, as on most standard camming units, then the compression load F would be shared among each of the two cams. The total outward force on the walls, however, would stay the same.
One may ask "Why not make µ larger, so the camming device will have a larger range of operation?." This question is answered next.
Figure 4 shows a diagram depicting the force that a cam exerts on the wall.
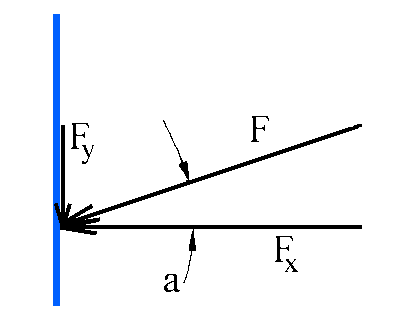
Figure 4
In order for the cam not to slide down the wall, the friction force Ff has to be enough to overcome Fy.
The friction force is the normal force Fx times the coefficient of friction, Cf.
Therefore, Ff > Fy where Ff = Fx*Cf.
Combining these two equations gives Cf > Fy/Fx.
Then, since Fy/Fx = tan(a), and a = tan-1µ we get the very interesting result: Cf > µ
Physically, this means that in a parallel crack, the coefficient of friction between the rock and the cams must be larger than µ or the cams will slide down the wall and the device will pull out of the crack. This is why µ cannot be increased indiscriminately. On the other hand, if µ is made too small, the range of the cams will not be very great, and the following forces will all increase: the compression force on the cams, the outward force on the walls, and the shear forces on the axle. Also, the ability of the device to work inside of a flared (non-parallel) crack will be limited, as will be shown next.
To summarize, for the placement of a camming device in a parallel crack:
r = eµø
a = tan-1(µ)
Fy = T/2
Fx = T/2µ
If µ = .25 then Fx = 2T
F = (T/2)*SQRT(1+1/µ2)
Placement of a Camming Device in a Flared Crack
Figure 5 shows the placement of a camming device in a flared (non-parallel) crack.
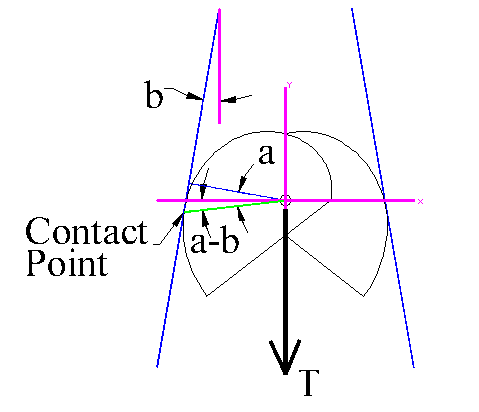
Figure 5
Notice that the angle of each wall is b so that the included angle between the two walls would be 2b.
It is apparent that the maximum flare that the device could work in would be when b = a, which for most camming devices currently used in rock climbing is about 14 degrees, so that the angle between the walls is about 28 degrees. If this angle is exceeded, the spring action of the cams would actually push the unit out of the crack.
Also notice that the angle of force against the wall (the green line) is still a! This means that theoretically the likelihood of slipping in a flared crack is not any greater than in a parallel walled crack! However, the forces involved may be greatly increased, as shown below. Also, in practice, other factors may come into play. For instance, if the cams did slip a little (say on the downside of a little bump) the resulting rapid acceleration of the device may be too fast for the spring action of the cams to reestablish contact with the rock. This is pure supposition, and would require a more detailed analysis than given here, or better yet, actual testing.
To determine the compression forces in the cams, and the forces on the axle, we proceed as in Figure 3 above, replacing angle a with angle a-b.
Summing forces in the vertical direction,
we get Fy = T/2.
Also, we know tan(a-b) = Fy/Fx.
Combining these two equations gives Fx = T/2tan(a-b).
Then, combining vectors, F = SQRT(Fx2 + Fy2)
Again, these forces are the total forces on each side. If there are two cams on each side, they will share these loads.
As an example, if µ = .25 (a = 14 degrees) and b = 7 degrees, then:
Fx = T/2tan(14-7) = 4.07T
If b = 13 degrees, then:
Fx = T/2tan(14-13) = 28.64T
A little experimentation shows that as the angle of the flare approaches the spiral angle (tan-1µ) the forces grow very large (theoretically infinite). There will be a large compression force on the cams, a large shear force on the axle, and a large spreading force on the walls of the crack.
Most likely, at these high forces, significant bending and/or deformation would take place so that the above equations would no longer be valid. Otherwise, it would be as Jardimedes said: "Give me a camming device in a properly flared crack and I will rip the world asunder."